After a solemn eleven month wait it is finally March again, which means it is finally not pathetic for me to reopen my code from last March to generate my March Madness bracket. In case you missed my post from last year about my bracket and algorithm you can find it here. In short, I participate in a March Madness pool that rewards players for correctly making picks that other players do not make. The two components are predicting the game correctly and predicting what other players will pick. I created a machine learning algorithm to terminate my competitors optimize my bracket.
In my follow-up March Madness post last year, I identified a few sources of error for my algorithm, one of which was correctly predicting which teams my competitors would pick. Since I had no data on how players behaved in my pool, I used data from ESPN. This ended up working very well since ESPN users picked only 2.1% different on average[1] than players in my pool. Still, I figured I could improve on this because ESPN users have a much stronger incentive to pick a favorite. This blog post details my attempt to model the picking behavior of other players in my pool.
Gathering Data
In order to fuel my machine learning algorithm I need data. Machine learning algorithms find patterns in past data to generate future predictions. My three major data sources were player picks in my pool, FiveThirtyEight’s tournament win probabilities, and pre-tournament AP rankings. These three data sources go back to 2014. I also had ESPN user picks for 2017. As is often the case with data analysis I spent about 80% of my time formatting the data and changing Jax State to Jacksonville St.
My end goal is to predict what percentage of players in my pool will choose team A to win in round X.[2] However, I decided to adjust the dependent variable I used in my machine learning to be the percentage of players picking a team above or below the team’s win probability from FiveThirtyEight. The reasons for adjusting the dependent variable are:
- The adjusted dependent variable has a nicer distribution. It has a more normal distribution which is often desirable in machine learning. See the two figures below. For example unadjusted, there are a lot of teams with nearly zero percent picked (all of the low seeds in the later rounds)
- While my bracket picking algorithm does use the unadjusted player pick percentage, the decisions are largely driven by unoptimal behavior of opposing players. As I explained in my post last year optimal behavior is choosing a team with the same likelihood as their win probability so any deviation from that is an inefficiency I can exploit. You can think of my new dependent variable (called over_under) as the amount other players over pick a team (positive number) or under a pick a team (negative number).

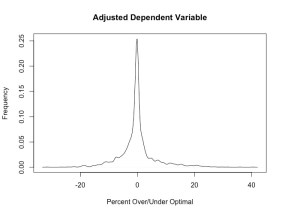
Figures 1 and 2. The figure on the left shows the distribution of the percentage picks, the percentage of players choosing team A to go to round X. There are many percentage picks near zero because middle and lower seeded teams are rarely picked to make later rounds. The second figure is shows the distribution of percentage pick – win probability. For example, let’s say 63% of people pick team A to make the Sweet 16 and FiveThirtyEight gives team A a 61% chance of making the Sweet 16. Then I would adjust to 63% – 61% = 2%
The major variables I used to predict my dependent variable were:
- Rank of team before beginning of NCAA tournament
- Seed of team in NCAA tournament
- FiveThirtyEight win probability in that round
- Whether the team was in a power conference
- The team’s regular season winning percentage
- The round of the game
The best predictor of whether a team was over picked or under picked were the seed and round, and I tried different combinations of variables in my models.
Algorithm Comparison
I tried five different models to predict the percentage each team would be over/under picked in each round. Four were machine learning models: random forest, lasso regression, gradient boosting machine, and neural net. The final model was using the ESPN user pick data. Each model was trained with 2014-2016 data and then validated with 2017 data. Since I only have ESPN user pick data from 2017, I only ran the ESPN model for that year. I tuned each model with 3-fold cross validation, using 2 years of data to predict the third year.
In order to improve the model’s performance I spent a lot of time tweaking the input variables. For example, I experimented with using round as a numeric and a categorical variable. When round is a numeric variable, rounds one and two have a closer relationship than one and three because the numbers one and two are closer than one and three. When it is categorical, each round treated individually, with no two rounds being more similar than any two other rounds.
My final results on the 2017 data are displayed below. Despite having a different scoring system, the ESPN user picks were actually better predictors than my machine learning models by about one percent.
Table 1. Error of Each Algorithm on 2017 Data
| Algorithm | Adjusted Mean Absolute Error[3] | Mean Absolute Error |
| ESPN User Picks | 2.1% | 2.1% |
| Random Forest | 2.9% | 3.0% |
| Neural Net | 3.2% | 3.4% |
| Gradient Boosting Machine | 3.8% | 4.0% |
| Lasso Regression | 3.8% | 4.2% |
While I am still not totally convinced that ESPN user picks are more accurate predictors because (1) ESPN users have a different scoring system and (2) I have a smaller sample size of ESPN data, it is an interesting result. I think one major reason ESPN user pick data is good, is because it is match up specific. Unlike my machine learning algorithm which predicts the percentage of individuals picking team A to go round X with no context of the possible matchups, ESPN users are making picks game by game and head-to-head. For example, this might be able to better account for a one seed who will likely face a tough four seed instead of an average four seed.
Conclusion
Even though I still have to see what the ESPN user pick data looks like this year and how it differs from my machine learning model, I am more inclined to use the ESPN user pick data. I did try starting with the ESPN User pick data and making small adjustments to improve its prediction accuracy, but I could not find a good model. It is interesting that even though ESPN users do not behave rationally for the ESPN scoring system, they behave close to rational for my pool’s scoring system.
Stay tuned for my next post later this week with my picks. If you would like to join my pool go to https://mayhem.ninja/ and register. The buy-in is $5. You can pay me or @dbeder on venmo.
[1] Mean absolute error.
[2] Since there are 64 teams and 6 rounds, that gives 6 x 64 = 384 observations for each year of data.
[3] Since the machine learning models predict the over_under variable “in a silo” some predictions are impossible because they mean that a team will be picked more than 100% or less than 0% of the time, or imply another impossibility. I adjusted the predictions to control for these impossibilities as much as possible. This is not an issue for the ESPN data.